retour sur p12 du livre pour la leçon
ou https://www.youtube.com/watch?v=LlLAIKiG4iQ
et https://www.youtube.com/watch?v=S7kjcOLolMM

II) Multiples, diviseurs d’un nombre.
On a :𝟔𝟖=𝟐×𝟑𝟒+𝟎 donc le reste de la division euclidienne de 68 par 2 est 0.
On dit que 2 et 34 divisent 68, que 68 est divisible par 2 et 34, que 68 est un multiple de 2 et 34.
On dit aussi que 2 et 34 sont des diviseurs de 68.
Définition : 𝒂 et 𝒃 sont des nombres entiers avec 𝒃≠𝟎.
On dit que 𝑏 est un diviseur de 𝑎 si le reste de la division euclidienne de 𝑎 par 𝑏 est nul.
C’est-à-dire que 𝒂=𝒃×𝒒 avec q un nombre entier.
On dit que 𝑏 divise 𝑎 ou que 𝑏 est un diviseur de 𝑎 ou que 𝑎 est divisible par 𝑏 ou que 𝑎 est un multiple de 𝑏.
15 n’est pas un diviseur de 732 car le reste de la division euclidienne de 732 par 15 est non nul et vaut 12.

exercices :
p18 n59 et 62 (voir critère de divisibilité)
p19 n73 (exercice utilisant un tableur, si vous n’avez qu’un équipement mobile et pas d’ordinateur il faudra télécharger un tableur)
p21n83 (exercice facile mais qui demande de la rigueur )

à lire pour résoudre le 83 et 73 :
Définition : pour tout couple (a, b) d’entiers naturels non nuls, on peut écrire le dividende a en fonction du diviseur b sous la forme a = bq + r où q (quotient) et r (reste) sont des entiers naturels uniques avec la condition r < b.
Avec Excel :

Placer le dividende dans la cellule A1 et le diviseur dans la cellule B1.
Le quotient est la partie entière de A/B. Taper dans B2 la formule = ENT(A1/B1) Taper =ENT( : montrer A1 ; taper / ; puis montrer B1 et enfin taper la parenthése suivie de la touche entrée.
Le reste, dans B2, se calcule facilement avec la formule modulo : = MOD(A1 ; B1).
Modifier les valeurs du dividende et du diviseur.

corrections à regarder en fin de semaine
n59
il faut utiliser le critère de divisibilité par 3 ; on conclu que ce nombre est divisible par 3 si il se termine par 1 ou 7.
n73

b) écrire :=a2+b2 dans la cellule c2
c) le reste est 18 donc il y a une erreur (mod(c2 ;97)
d) le bon numéro est
2690549588157
n83
u est la 21eme lettre donc
(21+1306478389561)/9 mais avec certaines calculatrices il y a un problème de capacité, vous trouvez un nombre entier or ce n’est pas le cas donc il faudra utiliser un tableur ou une calculatrice plus évoluée :
le reste est 1. donc le billet n’est pas valide.
exemple valide :U19216727123

pour ceux qui ont fini (projet tram de reins) :

aide :

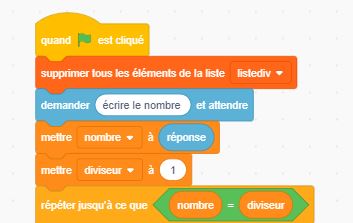
la correction sera posté en fin de semaine